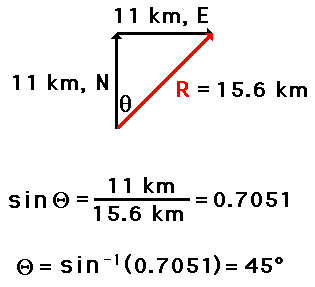
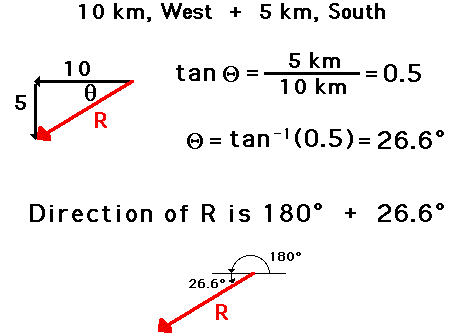
Wednesday, 19 September 2012
Tuesday, 4 September 2012
Free Fall, One Dimensional Motion with Constant Acceleration
Introduction to Free Fall:
.jpg)
Living young, wild and free. :)
Free fall is any motion of a body where its weight is the only force acting upon it. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward. Since free fall in the absence of forces other than gravity produces weightlessness or "zero-g," sometimes any condition of weightlessness due to inertial motion is referred to as free-fall. This may also apply to weightlessness produced because the body is far from a gravitating body. (Wikipedia)
Acceleration of Free Fall
The magnitude of this free fall acceleration is denoted by the symbol g, whose value slightly varies with the altitude and the latitude. The symbol g is also called as acceleration due to gravity. Near the surface of the Earth the g value is 9.8m/s^2. The free fall is a known example of uniformly accelerated movement, with an acceleration, a = -g = -9.8m/s2 (vertical axis pointing vertically upward). If you choose the vertical axis pointing vertically downward, the acceleration is taken as + 9.8m/s2. The kinematic equations for a rectilinear movement under the acceleration of gravity are the same as any movement with constant acceleration:
where Vf= final velocity Vi= initial velocity
t = time a= -g = acceleration due to gravity
Δy =displacement along the y-axis
sources: [http://www.jfinternational.com/ph/free-fall.html]
[http://www.physicsclassroom.com/class/1dkin/u1l5a.cfm]
.jpg)
Living young, wild and free. :)
Free fall is any motion of a body where its weight is the only force acting upon it. These conditions produce an inertial trajectory so long as gravity remains the only force. Since this definition does not specify velocity, it also applies to objects initially moving upward. Since free fall in the absence of forces other than gravity produces weightlessness or "zero-g," sometimes any condition of weightlessness due to inertial motion is referred to as free-fall. This may also apply to weightlessness produced because the body is far from a gravitating body. (Wikipedia)
A free falling object is an object that is falling under the sole influence of gravity. Any object that is being acted upon only by the force of gravity is said to be in a state of free fall. There are two important motion characteristics that are true of free-falling objects:
- Free-falling objects do not encounter air resistance.
- All free-falling objects (on Earth) accelerate downwards at a rate of 9.8 m/s^2
Examples of objects in free fall include:
- An object dropped at the top of a drop tube.
- An object thrown upward.
- The moon orbiting around the Earth. (Any planet or satellite is in free fall as their motion is caused entirely by gravity.)
History of Free Fall
The teachings of the great ancient wise Aristotle stating that heavy objects fall faster than light ones were accepted until the XVI Century. We know that if we drop a hammer and a feather or a sheet of paper from the same height, the hammer will reach first the ground. If we crumple the paper giving it a ball shape it is observed that both objects will reach the ground almost at the same time. It was the famous Italian physicist Galileo Galilei who refuted Aristotle's idea stating that, in absence of air resistance all objects fall with the same uniform acceleration. He cleverly proved his hypothesis using inclined planes getting a slower movement which could be measured with the rudimentary watches of that age. The slope of the planes could be increased gradually until reaching almost a vertical position allowing him to predict behavior of objects in free fall.
Acceleration of Free Fall
The magnitude of this free fall acceleration is denoted by the symbol g, whose value slightly varies with the altitude and the latitude. The symbol g is also called as acceleration due to gravity. Near the surface of the Earth the g value is 9.8m/s^2. The free fall is a known example of uniformly accelerated movement, with an acceleration, a = -g = -9.8m/s2 (vertical axis pointing vertically upward). If you choose the vertical axis pointing vertically downward, the acceleration is taken as + 9.8m/s2. The kinematic equations for a rectilinear movement under the acceleration of gravity are the same as any movement with constant acceleration:
where Vf= final velocity Vi= initial velocity
t = time a= -g = acceleration due to gravity
Δy =displacement along the y-axis
sources: [http://www.jfinternational.com/ph/free-fall.html]
[http://www.physicsclassroom.com/class/1dkin/u1l5a.cfm]
Subscribe to:
Comments (Atom)